When it comes to knowledge of the dynamics of fluid drift systems, the relation between strain and volume drift fee systems performs a vital position.This system enables engineers and researchers to analyze the conduct of fluids in various systems, offering precious insights into how strain and the flow rate interconnect. In this blog, we can delve into the intricacies of this courting, focusing on the eTAZ systems machine and its implications. By quitting this submission, you will understand how strain and extent glide prices are associated and how you can apply this knowledge to real-world scenarios.
The Basics of Pressure and Volume Flow Rate
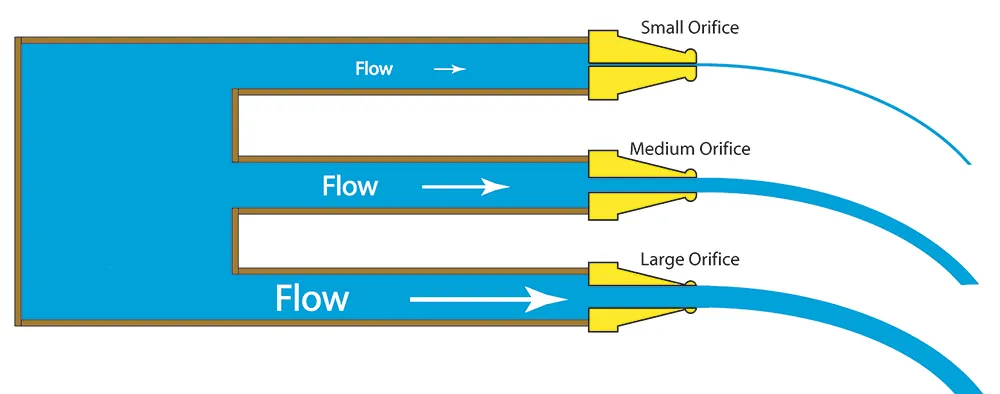
Foundational information on strain and volume drift rate is critical to navigating the complexities of fluid dynamics. Pressure is the force that a fluid exerts against the boundaries of its container or piping, defined by the pressure and volume flow rate within a given unit region. It is measured in units such as Pascals (Pa) or kilos per square inch (psi). This parameter is crucial in determining how fluid moves within its system. Volume drift fee, conversely, quantifies the quantity of fluid that moves past a specific factor inside the gadget in the course of a set time frame and is typically measured in cubic meters in keeping with 2nd (m³/s) or litres consistent with minute (L/min). The interaction between these two parameters underpins the operational principles of fluid mechanics, illustrating how alterations in you could immediately impact the opposite.
Introducing the eTAZ System
The eTAZ gadget represents a full-size jump ahead in the control and analysis of fluid drift dynamics. It employs a complicated ensemble of sensors and computational algorithms designed to offer an exceptional stage of control over each strain and quantity drift charge. This system can accomplish actual application, enabling users to make modifications on the fly to optimize the gadget’s overall performance. With its superior capabilities, the eTAZ machine stands at the leading edge of fluid dynamics generation. It offers a device that could drastically beautify the precision of measurements and the efficacy of gadget management. This innovation is particularly beneficial in applications where maintaining specific management over fluid movement is paramount, imparting a new degree of efficiency and accuracy.
Theoretical Foundations of the Pressure-Volume Flow Rate Relationship
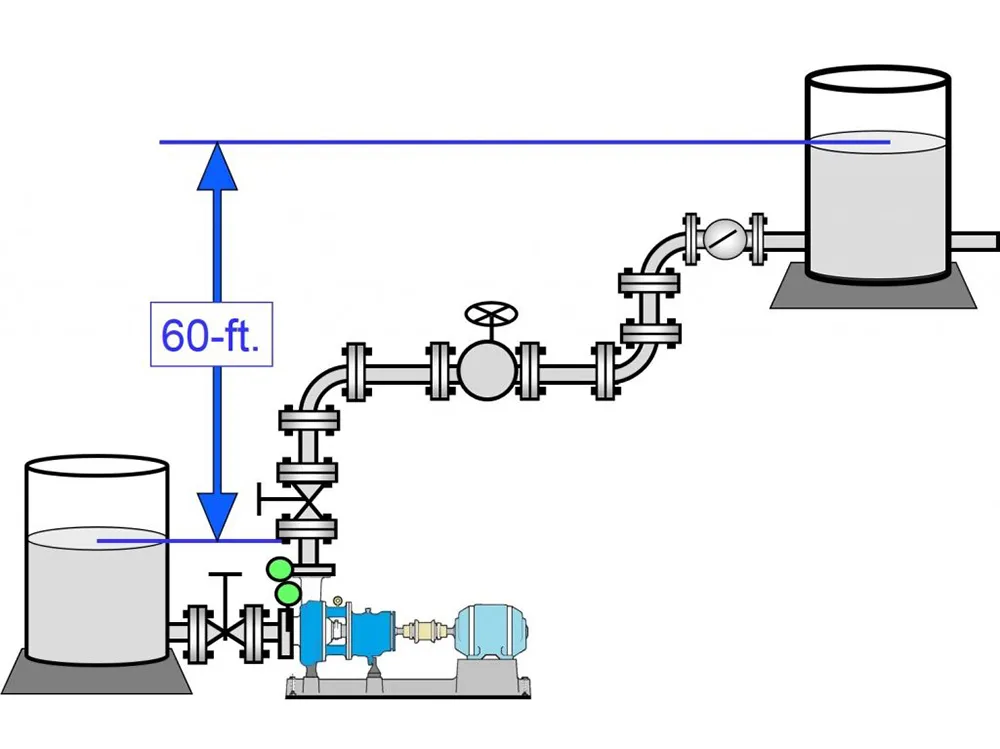
The complex relationship between quantity and pressure, which are related to flow charge, is at the core of fluid dynamics expertise. This relationship is profoundly understood by using Bernoulli’s equation. This fundamental principle states that a fluid’s pressure falls with increasing rate, creating an inverse relationship between the two measurements in a flowing device. For engineers and experts in fluid dynamics, this theoretical foundation is crucial because it provides a framework for predicting how changes in one parameter will impact changes in another. For instance, knowledge of how pressure variations can impact drift charge is crucial for systems that require control or manipulation of fluid velocity. Thus, Bernoulli’s equation provides a reasonable tool for understanding fluid dynamics and forms the basis of the fluid dynamics principle.
The Relation between Pressure and Volume Flow Rate Formula
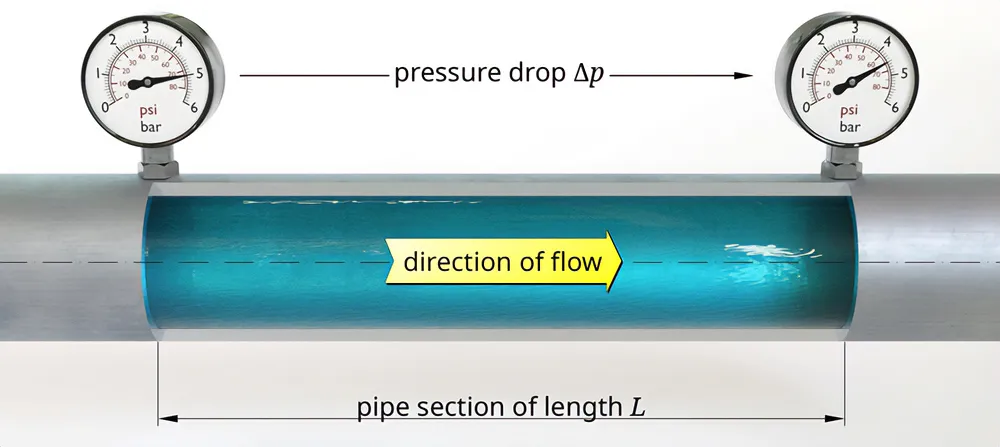
The formula encapsulating the connection between pressure and quantity waft fee is a cornerstone in fluid dynamics, permitting specific predictions and optimizations in fluid systems. It is succinctly captured using the equation Q = okay * √(ΔP). Q symbolizes the quantity float rate, and k represents a device-unique constant that includes the fluid’s residences and the machine’s geometry. ΔP is the pressure differential across the system. This equation underlines the direct but nonlinear connection between stress modifications and the resultant changes in float fee. Practically, even modest changes inside the stress differential can cause large versions of how fluid navigates through a gadget. This dating is instrumental for engineers designing and optimizing fluid float structures, allowing tweaking variables to attain the preferred glide fee efficiently.
Implications of the Pressure-Volume Relationship in eTAZ Systems
Integrating the stress-extent float fee relationship within eTAZ systems offers a groundbreaking technique for managing and controlling flumanagementamics. This critical courting allows the eTAZ machine to adjust to fluctuating conditions, ensuring fluid goes with the flow and stays optimal underneath varying pressures and volumes. This proactive adjustment capability is essential in environments where precision and reliability are paramount, together with production approaches, water treatment centres, and HVAC systems. The ability to instantly respond to modifications no longer most effectively complements the system’s performance but substantially reduces the chance of operational screw-ups and downtime. Moreover, by leveraging this relationship, the eTAZ device facilitates a sustainable operation, optimizing strength use and minimizing waste. This marks a new technology where we can control fluid dynamics with extraordinary accuracy and performance, representing a giant step forward in our potential to manage complicated fluid structures better.
Common Misconceptions and Challenges

Navigating the complexities of the connection between strain and extent flow price can be fraught with misconceptions and demanding situations which can preclude the effective management and analysis of fluid systems. One common false impression is the belief that this relationship is linear and straightforward, overlooking the nuanced interplay and the sizable impact that device-precise elements have on fluid dynamics. Another common false impression is underestimating the function of fluid residences and gadget geometry in figuring out the regular okay within the formula Q = okay * √(ΔP), which is critical for accurate calculations of float charge primarily based on stress differentials.
Challenges frequently emerge in the ideal size of pressure and extent of float charges, mainly in systems with complex geometries or in which fluids showcase non-ideal behaviour. Inaccuracies in those measurements can cause significant discrepancies in predicted and actual system performance. Additionally, implementing adjustments based on those measurements requires sophisticated control structures, just like the eTAZ machine, which might only be available in some settings. Overcoming these challenges necessitates a more profound know-how of fluid dynamics concepts, the adoption of advanced technological solutions, and a dedication to ongoing getting to know and model within the face of evolving system necessities and competencies.
Future Directions and Innovations

Fast advancements in the era are driving transformative modifications in the landscape of fluid dynamics. One specifically promising avenue is integrating artificial intelligence (AI) and devices to get to know fluid dynamics systems like the TAZ. These technologies can revolutionize how those systems reveal and manipulate fluid glide, bearing in mind more adaptive, intelligent responses to converting situations. AI should enable these structures to expect modifications in strain and extent to go with the flow rate earlier than they arise, providing preemptive changes that optimize performance and efficiency.
Moreover, developing more sophisticated sensor technology is another essential region of innovation. Enhanced sensors can offer higher consistency records regarding fluid conduct, capturing nuances that were formerly too diffuse to detect. This improvement in record quality can feed into more correct fashions of fluid dynamics, enabling the layout of more effective and efficient systems.
Conclusion
As we conclude our investigation into the complex link between amount drift charge and stress, we find that this dynamic is fundamental to fluid dynamics and essential for fluid structure design, analysis, and optimization. We’ve seen during the debate how this courting affects the performance of many packages, from basic ideas to the cutting-edge eTAZ device. The equation Q = okay * √(ΔP) serves as a link between theoretical understanding and practical application, enabling precise control of fluid behaviours under many circumstances. Furthermore, the potential for future advancements—primarily via the fusion of artificial intelligence and sophisticated sensor technology—emphasizes the ongoing development of fluid dynamics. Our ability to anticipate, control, and optimise fluid systems will surely make them more sophisticated as generation goes on.

Very interesting subject, thanks for putting up.Blog money
Pingback: Exploring an 30 Example of an Embedded System: eTAZ Systems -